(Current Sponsor: Department of Energy – Basic Energy Science) 

 

 

One of the most serious limitations in experimental dislocation studies is the invisibility of dislocations during mechanical tests. Of course, the current technology allows us to see the motion of dislocations in TEM in terms of in-situ straining tests. However, the sample thickness should be thin enough for the electron beam to be transparent. If the samples for the mechanical test are thicker than an electron transparent sample which is typically ~200 nm thick, there is no experimental way to see the evolution of dislocation structure in detail. Also, only dislocations which satisfy a certain diffraction condition are visible. Therefore, it is almost impossible to capture the dynamics of all dislocations at the same time. Furthermore, the velocity of dislocations is usually very fast under a conventional strain rate, so that it is difficult to record all the positions of dislocations with time. Even though all problems above are resolved, if the sample contains many dislocations, understanding the physical process becomes more difficult because we cannot handle the interaction between many dislocations analytically. Thus, we have needed a computational tool to enable us to track the positions of dislocations, to match the dislocation structures with those from the ex-situ TEM, and to study the local interaction between dislocations. Therefore, line dislocation dynamics simulation codes have been extensively developed to resolve these problems.

 

< 3-Dimensional Dislocation Dynamics (DD) >

A dislocation in line dislocation dynamics simulations (DD) is typically discretized by the node and the line, and all nodes satisfies the Frank’s rule (the sum of Burgers vector is zero with the line sense vectors flowing into the node). In isotropic elasticity, the stress field can be calculated from the analytical solutions. Especially, our simulation code uses the non-singular continuum theory developed by Prof. Wei Cai of Stanford University. Using the Peach-Koehler formula, the force on the discretization node can be obtained by employing the linear hat function. Then, the mobility law calculates the nodal velocity from the nodal force. The mobility law depends on the crystal structures, because the dislocations move on the different crystallographic planes for different crystal structures. Finally, new nodal positions can be updated by the time integration of nodal velocities. Then, a dislocation structure evolves to one at the next time step. Sometimes, the topological change is needed to allow dislocation interactions such as dislocation annihilation or junction formation. For the topological change, our code seeks a new local structure which produces the maximum power dissipation. Also, for the remeshing process, the nodes merge to reduce the computational load, or they split to obtain a better curvature of a curved dislocation. The DD code allows cross-slip process, too. However, atomic scale events such as jog and kink formation are limited because they requires the resolution of atomic distances such as molecular dynamics. 

Code Development Efforts)

• Parallel Dislocation Simulator (ParaDiS): ParaDiS (Parallel Dislocation Simulator)
• Dislocation Simulation code written by MatLab: DDLab
• Computer Simulations of Dislocations written by Wei Cai and Vasily Bulatov [link]

 

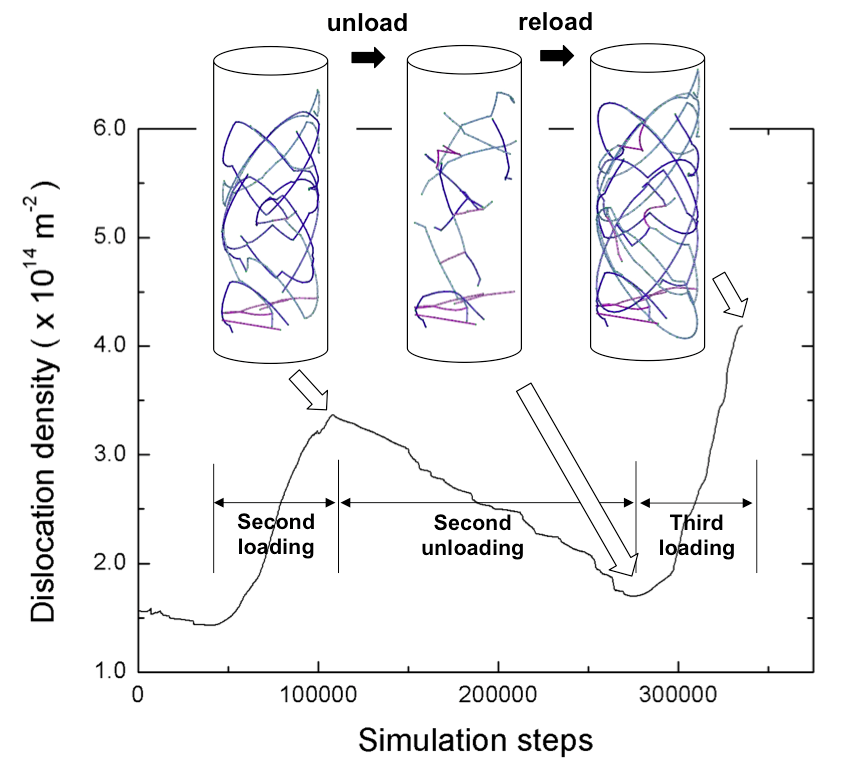
Cyclic loading in oxide-coated nanopillar

 

< Molecular Dynamics (MD) Simulation of Dislocations >

Molecular dynamics (MD) is a computer simulation method for studying the physical movements of atoms and molecules, and is thus a type of N-body simulation. The atoms and molecules are allowed to interact for a fixed period of time, giving a view of the dynamical evolution of the system. In the most common version, the trajectories of atoms and molecules are determined by numerically solving Newton’s equations of motion for a system of interacting particles, where forces between the particles and their potential energies are calculated using interatomic potentials or molecular mechanics force fields. The method was originally developed within the field of theoretical physics in the late 1950s but is applied today mostly in chemical physics, materials science and the modeling of biomolecules [Wikipedia].

 

Dislocation simulation in BCC nanopillars

(Gyuho Song, Seok-Woo Lee,“Effect of temperature on surface-controlled dislocation multiplication in body-centered-cubic metal micropillars,”Computational Materials Science 168, 172-179 (2019))

 

Related Publications

• Gyuho Song, Nicole K. Aragon, Ill Ryu, Seok-Woo Lee, “Low Temperature Failure Mechanism of [001] Niobium Micropillars Revealed by in-situ Cryogenic Micro-Tensile Tests and Dislocation Dynamics Simulations,” Journal of Materials Research (Invited Paper) (2021) – [PDF] [web]
• Gyuho Song, Seok-Woo Lee, “Effect of temperature on surface-controlled dislocation multiplication in body-centered-cubic metal micropillars,” Computational Materials Science 168, 172-179 (2019) [PDF] [web] 
• Seok-Woo Lee, Yintong Cheng, Ill Ryu, Julia R. Greer, “Cold-temperature deformation of nano-sized tungsten and niobium revealed by in-situ nano-mechanical experiments,” Science China Technological Sciences 16 184-189 (2014) (invited, and featured on the cover) [PDF][web].
• Seok-Woo Lee, Lucas Meza, Julia R. Greer, “Cryogenic nanoindentation size effect in [0 0 1]-oriented face-centered and body-centered-cubic single crystals,” Applied Physics Letters 103 101906 (2013) [PDF][web].
• Seok-Woo Lee, William D. Nix, “Size dependence of the yield strength of FCC and BCC metallic micropillars with diameters of a few micrometers,” Philosophical Magazine 92 1283-1260 (2012) [PDF][web].